Create a vector of bounding boxes

Bounding boxes denote the exten of geometries. It follows that bounding boxes are only defined for geometries that are located in space and have finite extent. Thus, vectors, lines, directions, rays, etc. does not have bounding boxes, while e.g. spheres, circles, segments, etc has. Since the extent of geometries cannot always be given exact (e.g. for circles), bounding boxes are defined in regular floating point precision. Bounding boxes can be compared for equality and be tested for whether they overlap. Adding bounding boxes together will give the bounding box containing both.

Usage

bbox(..., default_dim = 2)

is_bbox(x)

as_bbox(x)

Arguments

...

Either a vector of geometries or a range of numeric vectors (4 for 2D bounding boxes and 6 for 3D) interpreted in the order xmin, ymin, zmin, xmax, ymax, zmax.

default_dim

The dimensionality when constructing an empty vector

x

vector of bounding boxes or geometries

Value

An euclid_bbox vector

See also

Other non-geometry vectors: affine_transformation, exact_numeric()

Examples

# Construction
bbox(10, -2, 15, 0)
#> <2D bounding boxes [1]>
#> [1] <<10, -2>, <15, 0>>

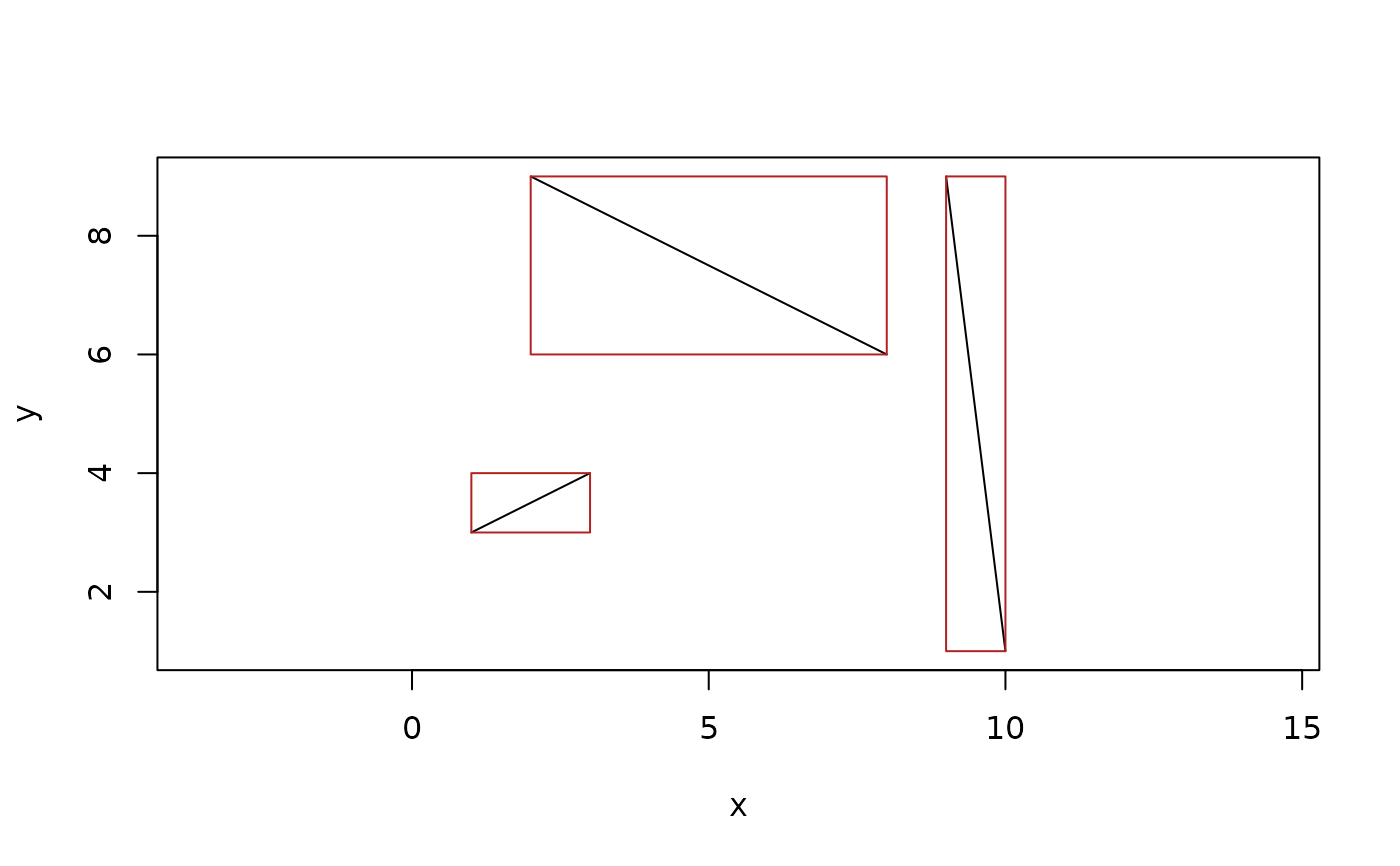
seg <- segment(point(sample(10, 4), sample(10, 4)),
               point(sample(10, 4), sample(10, 4)))

boxes <- bbox(seg)
boxes
#> <2D bounding boxes [4]>
#> [1] <<1, 3>, <3, 4>>  <<6, 8>, <6, 8>>  <<2, 6>, <8, 9>>  <<9, 1>, <10, 9>>

plot(seg)
euclid_plot(boxes, fg = "firebrick")


# Comparison
boxes[1] == boxes
#> [1]  TRUE FALSE FALSE FALSE

boxes[1:2] %is_intersecting% boxes[3:4]
#> [1] FALSE FALSE

# Addition
boxes[1] + boxes[2]
#> <2D bounding boxes [1]>
#> [1] <<1, 3>, <6, 8>>

cumsum(boxes)
#> <2D bounding boxes [4]>
#> [1] <<1, 3>, <3, 4>>  <<1, 3>, <6, 8>>  <<1, 3>, <8, 9>>  <<1, 1>, <10, 9>>

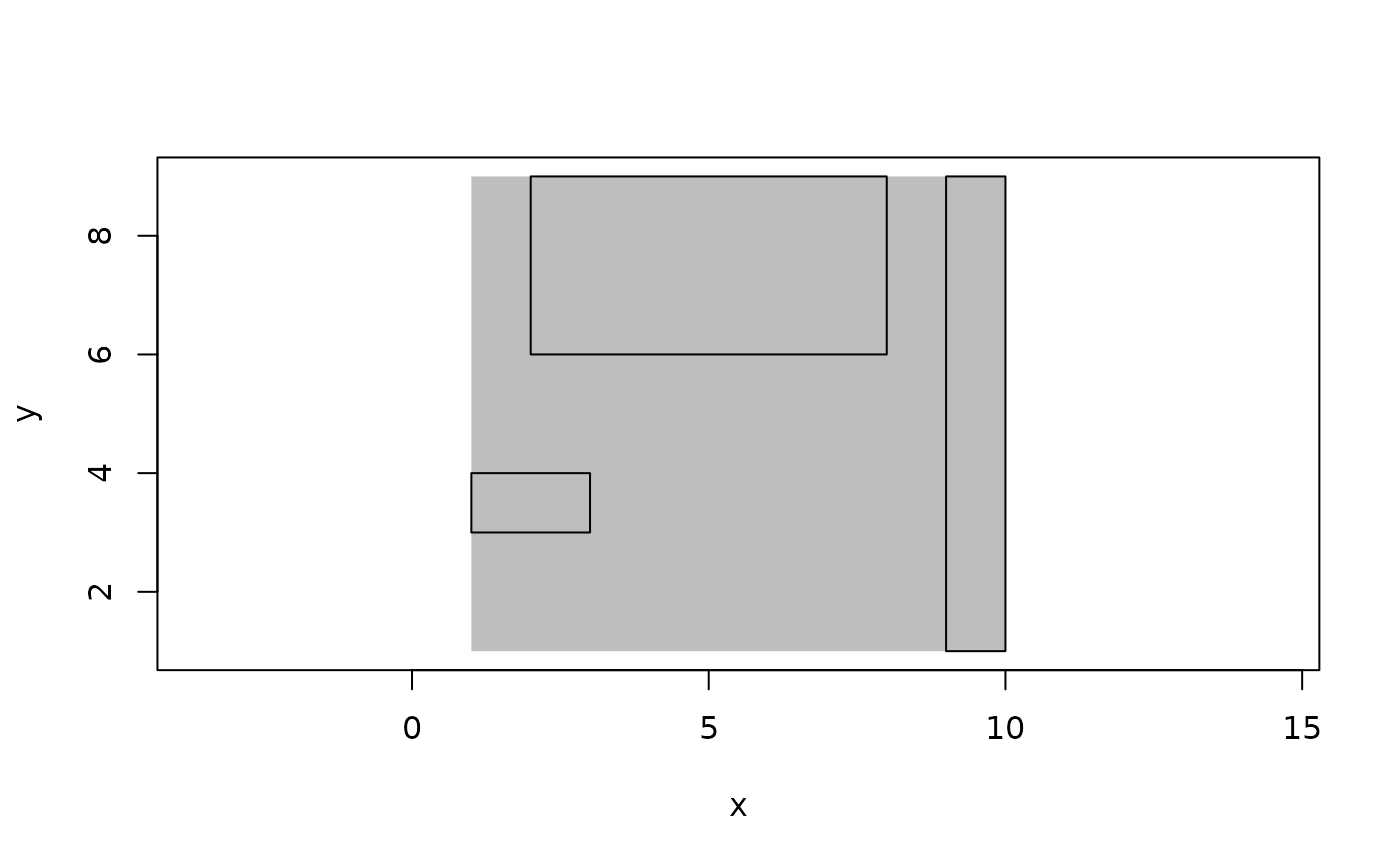
plot(sum(boxes), bg = "grey", fg = NA)
euclid_plot(boxes)


# Conversion
as.matrix(boxes)
#>      [,1] [,2] [,3] [,4]
#> [1,]    1    3    3    4
#> [2,]    6    8    6    8
#> [3,]    2    6    8    9
#> [4,]    9    1   10    9