The purpose of euclid is to provide a new unified foundation for computational geometry in R. It provides new data types for common low level geometric concepts such as lines, planes, points, triangles, etc. as well as a core of functionality relates to these primitives. Specialised geometric algorithms are intended to extend this package so that e.g. Tessellation will live in it’s own package but use the foundation laid out in euclid.
At its core euclid is an interface to the CGAL library for computational geometry. More specifically, it provides access to the functionality in the 2D and 3D Linear Geometry Kernel. The CGAL foundation means that computations with euclid are exact and free of the imprecision attached to working with floating point numbers. This is very important for geometry since floating point errors can compound and lead to failures in geometric predicates at the core of many geometric algorithms. To achieve this, data in euclid is never converted to R data structures but remain as pointers to CGAL structures unless specifically converted to numerics (in which case the floating point world kicks in)
Installation
For now, euclid can be installed from github using remotes:
# install.packages("remotes")
remotes::install_github("thomasp85/euclid")Data types
The core of euclid is a set of new primitive vector types that model 2 and 3 dimensional geometric objects. The following types are present:
Example
The following example shows how to work with the different data types:
library(euclid)
# Construct some exact numbers
random_num <- exact_numeric(rnorm(20))
# Exact numbers behave much like R numerics (though not everything is possible)
random_num[1:5]
#> <exact numerics [5]>
#> [1] -0.89691455 0.18484918 1.58784533 -1.13037567 -0.08025176
max(random_num)
#> <exact numerics [1]>
#> [1] 1.984474
random_num[2] * 10
#> <exact numerics [1]>
#> [1] 1.848492
random_num[5] + random_num[16]
#> <exact numerics [1]>
#> [1] -2.391321
sum(random_num)
#> <exact numerics [1]>
#> [1] 3.909221
# With exact numbers we can construct our geometries
p <- point(random_num[1:10], random_num[11:20])
p
#> <2D points [10]>
#> [1] <x:-0.897, y:0.418> <x:0.185, y:0.982> <x:1.59, y:-0.393>
#> [4] <x:-1.13, y:-1.04> <x:-0.0803, y:1.78> <x:0.132, y:-2.31>
#> [7] <x:0.708, y:0.879> <x:-0.24, y:0.0358> <x:1.98, y:1.01>
#> [10] <x:-0.139, y:0.432>
# Create a line based on a vector, going through the origin
l <- line(point(0, 0), vec(3, 7))
# Which points lies on the positive side of the line?
p %is_on_positive_side% l
#> [1] TRUE TRUE FALSE TRUE TRUE FALSE FALSE TRUE FALSE TRUE
# Project points to line
p1 <- project(p, l)
# Do the projected points lie on the line?
p1 %is_on% l
#> [1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
# Construct a triangle from a random point to the extremes of the projected points
t <- triangle(point(rnorm(1), rnorm(1)), min(p1), max(p1))
t
#> <2D triangles [1]>
#> [1] [<x:2.09, y:-1.2>, <x:-0.816, y:-1.9>, <x:0.675, y:1.57>]
# Which points lies inside the triangle?
p %is_inside% t
#> [1] FALSE FALSE TRUE FALSE FALSE FALSE TRUE FALSE FALSE FALSE
# Visualise result
plot(p, pch = 16)
euclid_plot(t)
euclid_plot(p[p %is_inside% t], cex = 3)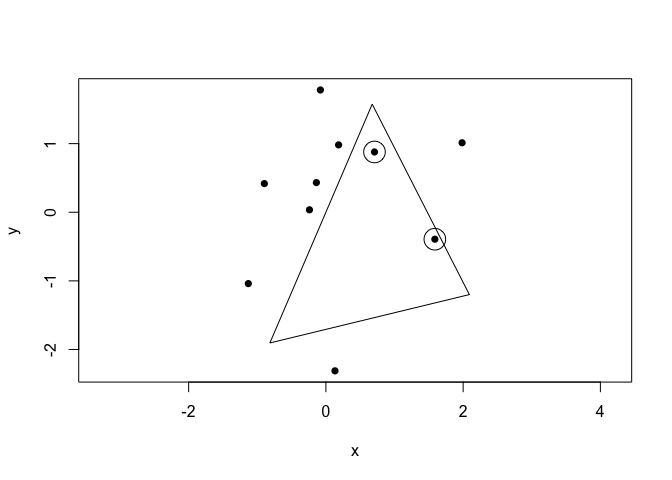
# Area of t (cannot be given exact for all geometries so is returned as numerics)
approx_area(t)
#> [1] -4.531123Code of Conduct
Please note that the euclid project is released with a Contributor Code of Conduct. By contributing to this project, you agree to abide by its terms.