Calculate radical point, line, or plane of two circles or spheres

The radical line or plane is the line (or plane) perpendicular to the line connecting the two circles or spheres and positioned such that at any point the tangent lines drawn to the two circles or spheres will have equal length. If the circles or sphere cross the radical will be positioned at the crossing points. It is not defined for cocentric circles and spheres. The radical point is defined as the intersection point of the three radical lines of three circles, or three radical planes of three spheres.

Usage

radical(x, y, z = NULL)

Arguments

x, y, z

vector of circles in 2D or spheres. If z is given the radical point will be computed

Value

A vector of lines or planes depending on the input

See also

Other Locations: barycenter(), bisector(), centroid(), circumcenter(), equidistant_line(), point(), weighted_point()

Examples

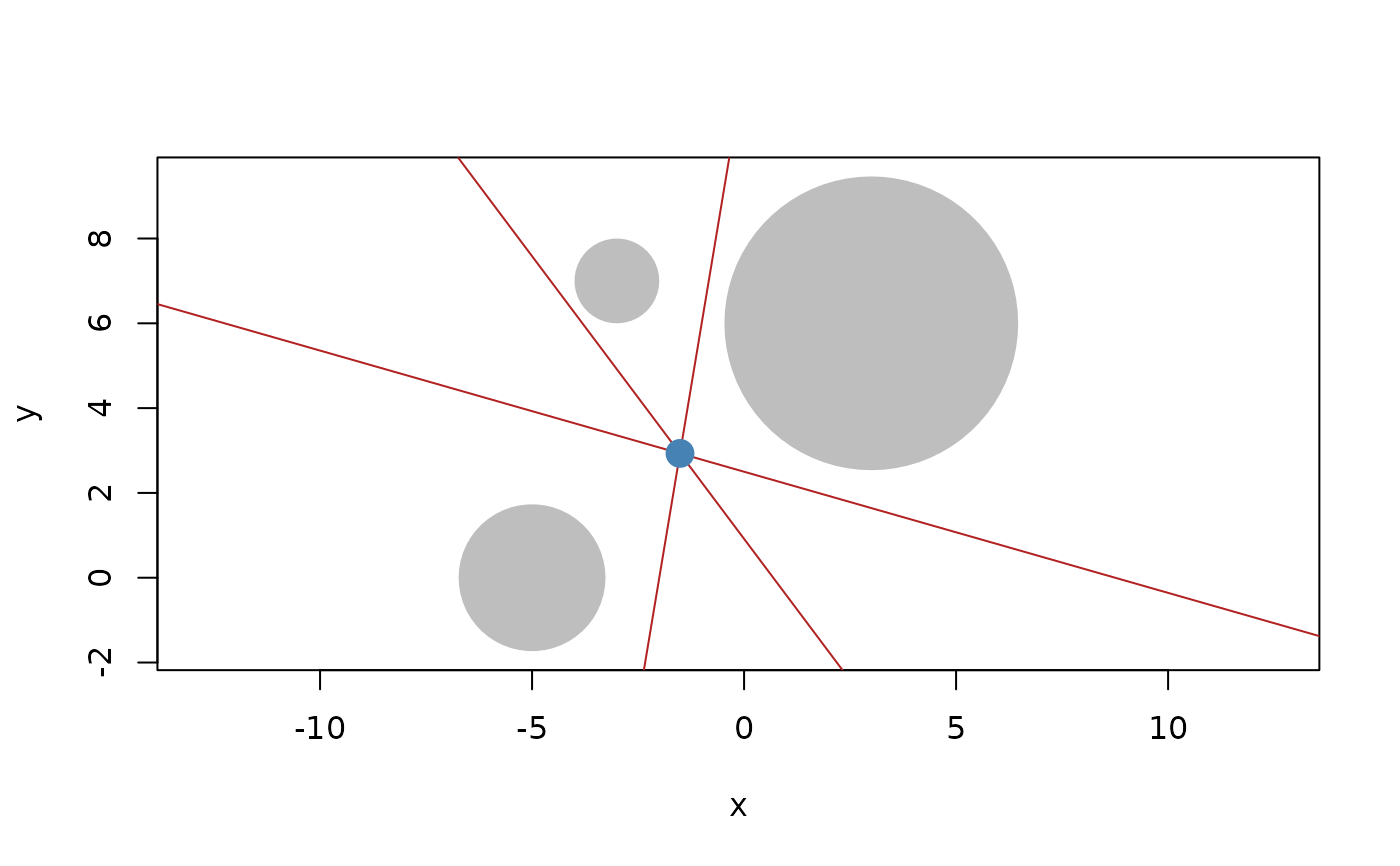
c1 <- circle(point(3, 6), 12)
c2 <- circle(point(-5, 0), 3)
c3 <- circle(point(-3, 7), 1)

# Radical line
radical(c1, c2)
#> <2D lines [1]>
#> [1] <a:-16, b:-12, c:11>

# radical point
radical(c1, c2, c3)
#> <2D points [1]>
#> [1] <x:-1.51, y:2.93>

plot(c(c1, c2, c3), bg = "grey", fg = NA)
euclid_plot(c(
  radical(c1, c2),
  radical(c2, c3),
  radical(c1, c3)
), col = "firebrick")
euclid_plot(radical(c1, c2, c3), pch = 16, cex = 2, col = "steelblue")


# Radical plane
radical(
  sphere(point(3, 6, 3), 12),
  sphere(point(-6, 2, 7), 3)
)
#> <3D euclid_planes [1]>
#> [1] <a:-18, b:-8, c:8, d:-44>