Vector of iso rectangles

Iso rectangles are axis aligned rectangles mimicking bounding boxes but given by exact numerics (bounding boxes are defined by floats because not all geometries have exact defined extent). Internally they are stored as two points giving the bottom-left and top-right corner of the rectangle. Iso rectangles are considered degenerate all its vertices are colinear.

Usage

iso_rect(...)

is_iso_rect(x)

as_iso_rect(x)

Arguments

...

Various input. See the Constructor section.

x

A vector of iso rectangles or an object to convert to it

Value

An euclid_iso_rect vector

Constructors

2 dimensional iso rectangles

• Providing a bbox will create iso rectangles matching the bbox

• Providing two points will create iso rectangles with the points as diagonal opposite vertices

• Providing 4 numeric will construct iso rectangles with the given extent, with the numerics being interpreted in the following order: left, bottom, right, top

See also

Other Geometries: circle(), direction(), iso_cube(), line(), plane(), point(), ray(), segment(), sphere(), tetrahedron(), triangle(), vec(), weighted_point()

Other Surfaces: circle(), plane(), triangle()

Examples

# Construction
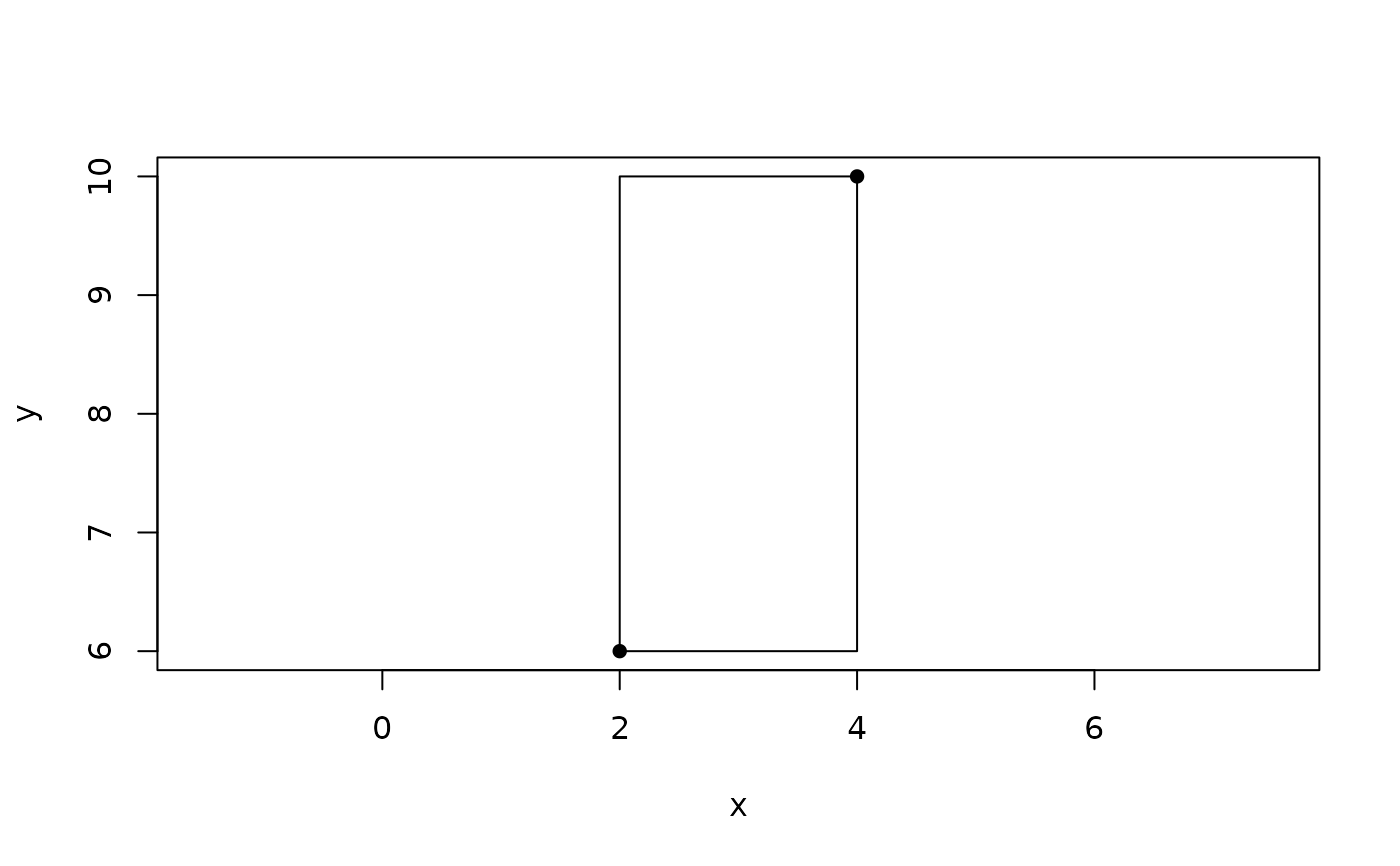
p <- point(sample(10, 2), sample(10, 2))
r <- iso_rect(p[1], p[2])
r
#> <2D euclid_iso_rects [1]>
#> [1] [<x:2, y:6>, <x:4, y:6>, <x:4, y:10>, <x:2, y:10>]

plot(r)
euclid_plot(p, pch = 16)


r <- iso_rect(4, 10, 7, 16)
plot(r, bg = "grey", fg = NA)
abline(v = 4, lty = 2)
abline(v = 7, lty = 2)
abline(h = 10, lty = 2)
abline(h = 16, lty = 2)


circ <- circle(point(5, 9), 13)
iso_rect(bbox(circ))
#> <2D euclid_iso_rects [1]>
#> [1] [<x:1.39, y:5.39>, <x:8.61, y:5.39>, <x:8.61, y:12.6>, <x:1.39, y:12.6>]